A Karnaugh map (K-map) is a graphical tool used to simplify Boolean algebra expressions. It provides a visual method of grouping together expressions with common factors, which makes it easier to minimize complex logical expressions without having to use extensive Boolean algebra calculations. Below is the Karnaugh Map Solver (Visualization Tool) for solving expressions.
Karnaugh Map Solver (K-Map) Visualization Tool
Truth Table Input
Steps to Use a K-Map
- Create the Map: Draw a grid based on the number of variables. For example, with 3 variables (A, B, and C), the K-map will have 8 cells (since 23 = 8).
- Fill the Map: Place the output values into the corresponding cells. (or)
- You can also input the K-map fields using our truth table input. Just enter the fields in csv format and hit generate K-Map.
- Remember the Generate K-Map button works if you have entered the truth table values.
- Group the Cells: Identify groups of 1s (or 0s for POS simplification). These groups must be rectangular and can include 1, 2, 4, 8, etc., cells. Larger groups provide more simplification.
- Write the Simplified Expression: Based on the groups, write down the simplified Boolean expression.
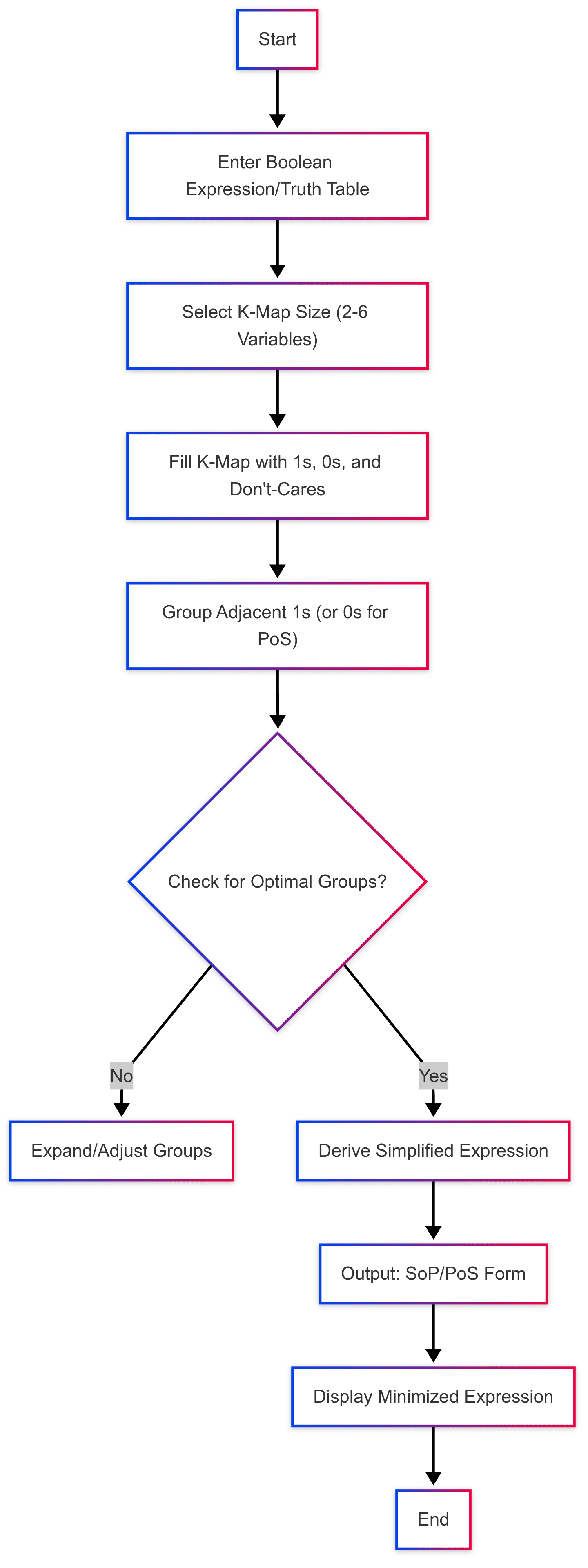
Step-by-Step Examples
Example1: Simplifying a Boolean Expression
Let’s simplify the Boolean expression A′B′C + AB′C + ABC′A’B’C + AB’C + ABC’A′B′C + AB′C + ABC′ using the Karnaugh Map:
- Mapping Minterms: Place the minterms A′B′CA’B’CA′B′C, AB′CAB’CAB′C, and ABC′ABC’ABC′ on a 3-variable K-map.
- Grouping: Identify and group adjacent cells (minterms that differ by only one variable).
- Simplified Expression: The groups correspond to simplified terms. Here, A′B′C + AB′C + ABC′A’B’C + AB’C + ABC’A′B′C + AB′C + ABC′ simplifies to B′C + AC′B’C + AC’B′C + AC′, reducing the number of gates needed.
Example 2: Handling Don’t Care Conditions
For a function with a don’t-care condition, such as A′B′ + ABC + A′B′C′ + D′A’B’ + ABC + A’B’C’ + D’A′B′ + ABC + A′B′C′ + D′:
- Mapping: Plot the function on the K-map, including the don’t care conditions.
- Grouping: Group the cells with 1s, using don’t-care conditions to form larger groups, leading to more simplification.
- Simplified Expression: The result could simplify to A′B′ + C′DA’B’ + C’DA′B′ + C′D, further reducing the logic complexity by taking advantage of the don’t-care conditions.
Key Features
- Grid Format: A K-map is typically arranged in a grid format, with each cell representing a possible combination of input variables.
- Number of Cells: The number of cells in a K-map is 2n , where n is the number of input variables.
- Grouping: Adjacent cells (cells next to each other) represent expressions that differ by only one variable. These can be grouped together to simplify the overall expression.
- Minimization: By grouping ones (or zeros) in the K-map, you can create a simplified Boolean expression.
Related Articles
- Depth First Search Algorithm
- ClipDrop AI
- Prim’s Algorithm
- BMI Calculator by Age and Gender
- Prim’s Algorithm in DAA
- Horspool’s Algorithm in DAA
- Kadane’s Algorithm
- Knapsack Problem using Branch and Bound
- Kruskal’s Algorithm (MST)
- Classic Snake Game using Java
- Fake Coin Problem
- Advanced Meme Generator
- Remaker AI Face Swap Tool
- Floyd-Warshall Algorithm
- Whack a Mole game using JavaScript
FAQ's
- Choose the K-map based on how many variables there are.
- Determine the problem’s minimum and maximum terms.
- Put 1s in K-map blocks corresponding to the minterms for SOP (0s elsewhere).
- Put 0s in K-map blocks corresponding to the maxterms for POS (1s elsewhere).
The algebraic expressions in Boolean functions can be made simpler visually using a Karnaugh map, or K-map, without the need for complex theorems or equation manipulation.
A three variable K-Map consists of eight (23) squares, or cells, where each square denotes a minterm of a maxterm.
The designation of the minterm or maxterm is indicated by the small number in the lower right corner of each cell.
K-map uses gray code in order to simplify Boolean expressions. Rather than being in binary numerical order, the row and column indices (displayed across the top and down the left side of the K-map) are ordered in gray code.
5 thoughts on “Karnaugh Map Solver”