Table of Contents
Introduction
Kruskal’s algorithm looks at a minimum spanning tree of a weighted connected graph G = [V, E] as an acyclic subgraph with |V| − 1 edges for which the sum of the edge weights is the smallest. (It is not difficult to prove that such a subgraph must be a tree.) Consequently, the algorithm constructs a minimum spanning tree as an expanding sequence of subgraphs that are always acyclic but are not necessarily connected on the intermediate stages of the algorithm.
The algorithm begins by sorting the graph’s edges in nondecreasing order of their weights. Then, starting with the empty subgraph, it scans this sorted list, adding the next edge on the list to the current subgraph if such an inclusion does not create a cycle and simply skipping the edge otherwise.
ALGORITHM Kruskal(G)
//Kruskal’s algorithm for constructing a minimum spanning tree
//Input: A weighted connected graph G = [V, E]
//Output: ET , the set of edges composing a minimum spanning tree of G
sort E in nondecreasing order of the edge weights w(ei1) ≤ … ≤ w(ei|E|)
ET ← ∅; ecounter ← 0 //initialize the set of tree edges and its size
k ← 0 //initialize the number of processed edges
while ecounter < |V| − 1 do
k ← k + 1
if ET ∪ {eik} is acyclic
ET ← ET ∪ {eik}; ecounter ← ecounter + 1
return ET
The correctness of Kruskal’s algorithm can be proved by repeating the essential steps of the proof of Prim’s algorithm given in the previous section. The fact that ET is actually a tree in Prim’s algorithm but generally just an acyclic subgraph in Kruskal’s algorithm turns out to be an obstacle that can be overcome.
The below image demonstrates the application of Kruskal’s algorithm to the same graph we used for illustrating Prim’s algorithm.
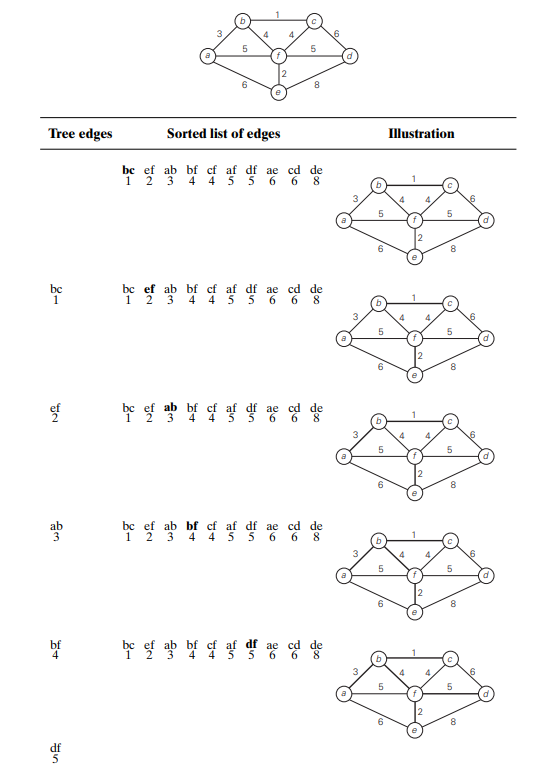
- As you trace the algorithm’s operations, note the disconnectedness of some of the intermediate subgraphs. Applying Prim’s and Kruskal’s algorithms to the same small graph by hand may create the impression that the latter is simpler than the former.
- This impression is wrong because, on each of its iterations, Kruskal’s algorithm has to check whether the addition of the next edge to the edges already selected would create a cycle.
- It is not difficult to see that a new cycle is created if and only if the new edge connects two vertices already connected by a path, i.e., if and only if the two vertices belong to the same connected component.
Note: Each connected component of a subgraph generated by Kruskal’s algorithm is a tree because it has no cycles.
Check the below image for a new edge connecting two vertices.
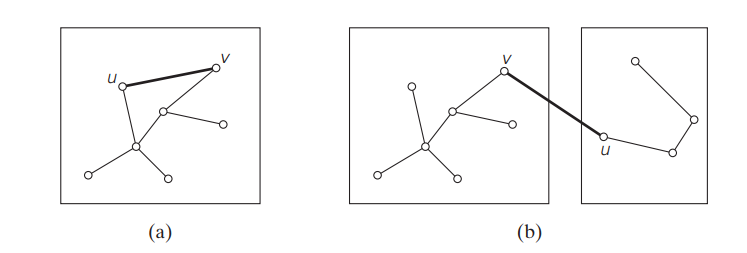
Observations of Kruskal's Algorithm
- In view of these observations, it is convenient to use a slightly different interpretation of Kruskal’s algorithm. We can consider the algorithm’s operations as a progression through a series of forests containing all the vertices of a given graph and some of its edges.
- The initial forest consists of |V | trivial trees, each comprising a single vertex of the graph. The final forest consists of a single tree, which is a minimum spanning tree of the graph.
- On each iteration, the algorithm takes the next edge (u, v) from the sorted list of the graph’s edges, finds the trees containing the vertices u and v, and, if these trees are not the same, unites them in a larger tree by adding the edge (u, v).
- Fortunately, there are efficient algorithms for doing so, including the crucial check for whether two vertices belong to the same tree. They are called union find algorithms.
Conclusion
With an efficient union-find algorithm, the running time of Kruskal’s algorithm will be dominated by the time needed for sorting the edge weights of a given graph. Hence, with an efficient sorting algorithm, the time efficiency of Kruskal’s algorithm will be in O(|E| log |E|).
References
FAQ'S
One well-known method for determining a graph’s minimum spanning tree is Kruskal’s algorithm. The fact that the edges of a minimum spanning tree must comprise a subset of the edges of any other spanning tree is exploited by this greedy algorithm.
The prim’s algorithm starts by choosing the root vertex and moves proximally from vertex to vertex. Conversely, starting from the smallest weighted edge, Kruskal’s algorithm aids in the creation of the minimum spanning tree.
Both the Dijkstra and the Kruskal algorithms are members of the greedy algorithm family. The minimum covering graph problem is solved using the Kruskal algorithm, while the shortest path problem is solved using the Dijkstra algorithm.
There are two components to the proof:
- Firstly, the algorithm’s ability to produce a spanning tree.
- Secondly, the minimal weight of the constructed spanning tree.
