Huffman coding algorithm in daa stands out as a pivotal algorithm in the world of lossless data compression. This ingenious method employs a variable-length code for different characters, ingeniously mapping frequency of use to the length of the code.
Characters that appear more frequently are assigned shorter codes, while those that occur less frequently receive longer codes. This approach ensures optimal efficiency in data compression.
The process of Huffman coding can be broadly divided into two distinct phases:
- Creation of the Huffman Tree
- Traversal of the Huffman Tree to Derive Codes
It’s also called variable-length encoding, when we encode different symbols with different codewords of varying lengths.
Practical Example
Let’s dive into the concept of Huffman coding algorithm in daa with a simple example. Consider the string YYYZXXYYX:
- The character Y appears the most frequently.
- X follows in frequency.
- Z appears the least frequently.
In accordance with Huffman coding principles, Y would be assigned the shortest code, X a slightly longer code, and Z, the least frequent character, would receive the longest code among the three.
Computational Complexity
The time complexity of Huffman coding in assigning codes based on character frequency stands at O(n log n). This efficiency makes it a staple in data compression techniques, offering a blend of simplicity and effectiveness.
Enhancing Data Compression with Huffman Coding
Huffman coding’s method of assigning variable-length codes to characters based on their frequencies is a cornerstone of efficient data compression. By prioritizing the most common characters with shorter codes, it minimizes the overall size of the data, making it an essential algorithm in the field of computer science and information technology.
This algorithm not only optimizes data storage but also plays a crucial role in network communication, where efficient data transmission is key. Its implementation can lead to significant bandwidth savings and improved speed in data transfer across the internet.
Below is an Example that you can understand better.
Huffman Coding Algorithm in DAA
Step 1: To create a system that can understand and process information, we must start by organizing the symbols we’ll work with. We do this by creating “node trees” and assigning each tree a symbol from the alphabet. We also track how often each symbol appears so we can give it a weight or level of importance.
Step 2: Continue the process until only one tree remains. Locate two trees with the lowest weight and designate them as the left and right subtrees of a fresh tree. The sum of their weights should be recorded in the new tree’s root as its weight.
The constructed tree above in the figure is called the Huffman tree. It defines a Huffman code in the manner described above.
Example: Consider an example of a five-symbol alphabet {A, B, C, D, _} with the frequency occurrence in a text made up of these symbols:

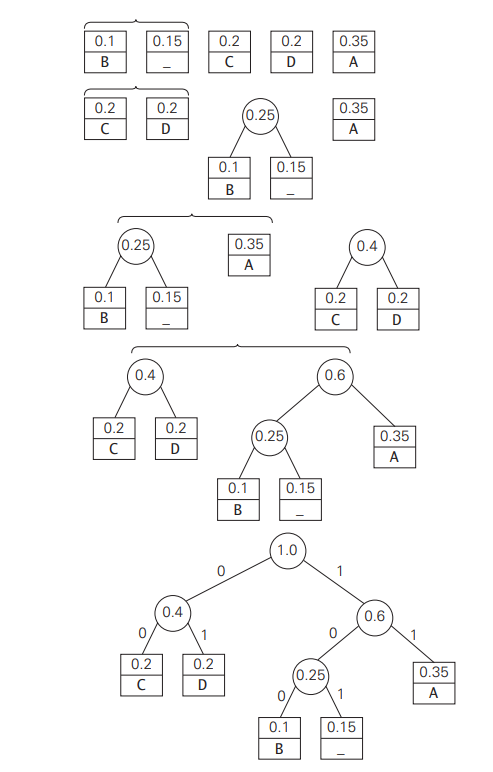
The results code words are as follows;
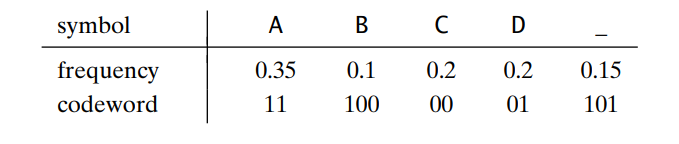
Hence, we encode DAD as 011101, and 10011011011101 can be decoded as BAD_AD. With the frequency occurrence given and the codeword lengths obtained;
The average bits per symbol in the code will be:
2 * 0.35 + 3 * 0.1 + 2 * 0.2 + 2 * 0.2 + 3 * 0.15 = 2.25
Understanding the complexity of Huffman Coding can be challenging. However, resources like Huffman Coding Algorithm in DAA provide comprehensive insights and step-by-step guides that make learning this algorithm accessible to both beginners and seasoned programmers alike.
- Huffman coding stands as a cornerstone of lossless data compression, enabling efficient storage and transmission of information.
- Its ability to minimize file sizes without losing data integrity makes it a valuable tool in the digital age.
- For those interested in exploring this fascinating algorithm further, detailed guides serve as excellent starting points, offering insights into the practical implementation and underlying theory of Huffman Coding Algorithm in DAA.
Huffman Coding compared to other Compression Algorithms
Huffman Coding is just one of many data compression algorithms, and each has its own strengths and weaknesses. Let’s compare it to a few other popular compression methods:
- Run-Length Encoding (RLE):
- Idea: Replace consecutive repeated characters with a count.
- Pros:
- Simple and easy to implement.
- Works well for data with long runs of identical characters (e.g., bitmap images).
- Cons:
- Inefficient for data with frequent changes (e.g., text files).
- Doesn’t handle random patterns efficiently.
- Lempel-Ziv-Welch (LZW):
- Idea: Build a dictionary of frequently occurring patterns and replace them with shorter codes.
- Pros:
- Adaptive: The dictionary grows as it encounters new patterns.
- Efficient for compressing text and other structured data.
- Cons:
- Requires more memory for the dictionary.
- Patent issues (historically).
- Arithmetic Coding:
- Idea: Encode entire messages as fractional values in a range.
- Pros:
- Theoretically optimal compression (can achieve entropy limit).
- Handles probabilities of individual symbols.
- Cons:
- More complex to implement.
- Sensitive to precision errors.
- Burrows-Wheeler Transform (BWT) with Move-to-Front (MTF) and Run-Length Encoding:
- Idea: Rearrange data to group similar characters together, then apply RLE.
- Pros:
- Effective for compressing repetitive data (e.g., DNA sequences).
- Used in algorithms like bzip2.
- Cons:
- Still not as widely used as Huffman or LZW.
- Deflate (used in ZIP and PNG):
- Idea: Combines LZ77 (similar to LZW) and Huffman Coding.
- Pros:
- Efficient and widely supported.
- Good balance between compression ratio and speed.
- Cons:
- Slightly slower than pure Huffman or LZW.
- Huffman Coding:
- Pros:
- Simple and efficient.
- Guarantees optimal prefix-free codes.
- Widely used in practice (e.g., in ZIP, JPEG, and MP3).
- Cons:
- Requires a priori knowledge of character frequencies.
- Not adaptive (doesn’t adjust to changing data).
- Pros:
In summary, each algorithm has its trade-offs. Huffman Coding is great for static data where character frequencies are known in advance. For dynamic data or when you need adaptability, other algorithms like LZW or Deflate might be better choices.
Related Articles
- Depth First Search Algorithm
- ClipDrop AI
- Prim’s Algorithm
- BMI Calculator by Age and Gender
- Prim’s Algorithm in DAA
- Horspool’s Algorithm in DAA
- Kadane’s Algorithm
- Knapsack Problem using Branch and Bound
- Kruskal’s Algorithm (MST)
- Classic Snake Game using Java
- Fake Coin Problem
- Advanced Meme Generator
- Remaker AI Face Swap Tool
- Floyd-Warshall Algorithm
- Whack a Mole game using JavaScript
FAQ's
Huffman Coding is a method of compressing data independent of data type.
- Calculate the frequency of each string.
- Sort the characters based on their frequencies in ascending order.
- Make a unique character like the leaf code.
- Create an internal node.
Huffman Coding finds practical applications in various domains.
- File Compression
- Transmission Systems
- Multimedia Formats
- Text and Fax Transmission
An algorithm called Huffman coding is used to compress data in order to minimize its size without sacrificing any of its details. David Huffman is the person who developed this algorithm. When we wish to compress data that contains frequently occurring characters, Huffman coding is usually helpful.