Radix Sort Algorithm is a non-comparative sorting algorithm that sorts numbers by processing individual digits. It works by sorting the numbers based on each digit, starting from the Least Significant Digit (LSD) to the Most Significant Digit (MSD) or vice versa. The algorithm leverages a stable subroutine (usually counting sort) to sort the digits at each significant place value.
Steps of Radix Sort Algorithm
- Determine the Maximum Number of Digits: Find the maximum number of digits (d) in the largest number in the list. This helps determine the number of passes required to sort all numbers.
- Sort by Each Digit: Starting from the least significant digit (LSD) to the most significant digit (MSD), sort the numbers based on the current digit. A stable sorting algorithm like counting sort is used for each digit to maintain the relative order of numbers with the same digit.
Radix Sort Visualization Tool
Example Array
Lest consider an array [329, 457, 657, 839, 436, 720, 355]
Pass 1: Sorting by 1s Place
- We start by looking at the rightmost digit of each number.
- We group the numbers based on these digits into buckets (0-9).
- We then concatenate these buckets to form the array for the next pass.

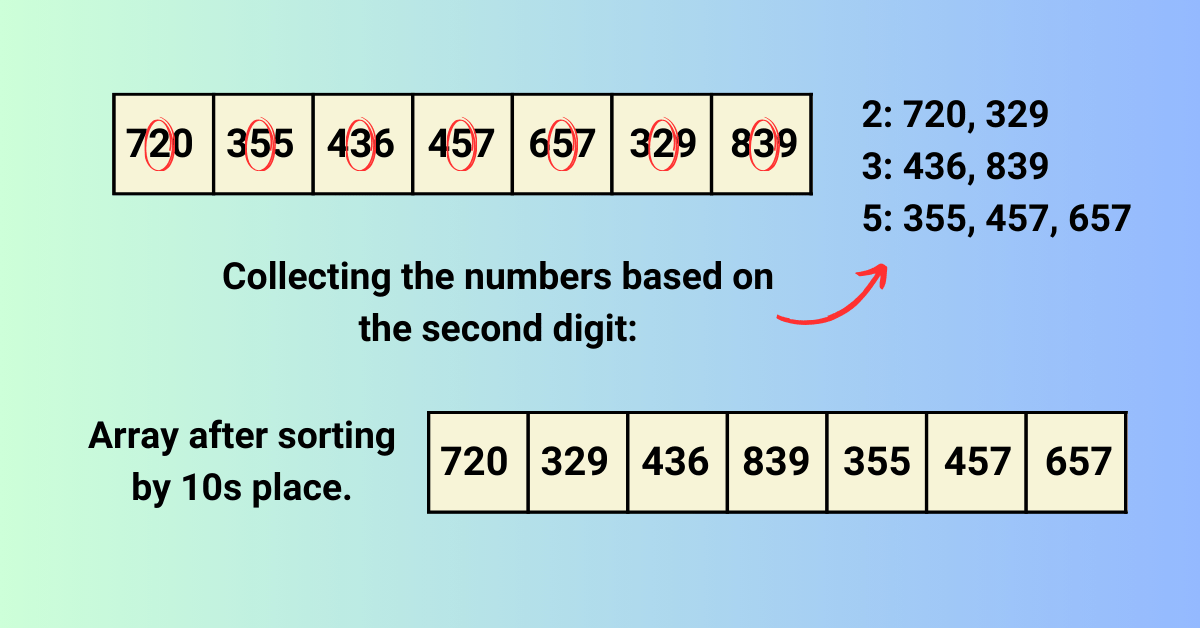
Pass 2: Sorting by 10s Place
- Now, we consider the second digit from the right (10s place).
- Using a stable sort (e.g., counting sort), we sort the array based on these digits.
- Again, we group the numbers into buckets (0-9) based on the 10s place digit and concatenate these buckets.
Pass 3: Sorting by 100s Place
- Finally, we sort by the leftmost digit (100s place).
- We sort the array using a stable sort based on these digits.
- After grouping the numbers into buckets (0-9) and concatenating them, we get the final sorted array.


Pseudocode for Radix Sort Algorithm
function radixSort(arr):
maxNumber = findMax(arr)
numDigits = numberOfDigits(maxNumber)
for digitPlace from 1 to numDigits:
arr = countingSortByDigit(arr, digitPlace)
return arr
function findMax(arr):
max = arr[0]
for each number in arr:
if number > max:
max = number
return max
function numberOfDigits(number):
count = 0
while number != 0:
number = number // 10
count += 1
return count
function countingSortByDigit(arr, digitPlace):
n = length of arr
output = array of size n
count = array of size 10 initialized to 0
for i from 0 to n-1:
digit = (arr[i] // digitPlace) % 10
count[digit] += 1
for i from 1 to 9:
count[i] += count[i - 1]
for i from n-1 to 0:
digit = (arr[i] // digitPlace) % 10
output[count[digit] - 1] = arr[i]
count[digit] -= 1
for i from 0 to n-1:
arr[i] = output[i]
return arr
→ Explanation of Each Function:
- radixSort(arr):
- This is the main function that performs Radix Sort on the array arr.
- It first finds the maximum number in the array to determine the number of digits (numDigits).
- Then, it iterates over each digit place (1s, 10s, 100s, etc.) and sorts the array using countingSortByDigit function for each digit place.
- findMax(arr):
- This function finds and returns the maximum number in the array arr.
- It initializes max to the first element and then iterates over the array to update max if a larger number is found.
- numberOfDigits(number):
- This function calculates the number of digits in a given number.
- It repeatedly divides the number by 10 until it becomes 0, counting the number of divisions.
- countingSortByDigit(arr, digitPlace):
- This function performs a stable sort (counting sort) on the array arr based on the digit at digitPlace.
- It initializes an output array to store the sorted array and a count array to keep track of the frequency of each digit (0-9).
- It calculates the digit at digitPlace for each number and updates the count array.
- It modifies the count array to hold the actual position of each digit in the output array.
- It builds the output array by placing each number at its correct position based on the digit.
- Finally, it copies the output array back to the original array arr.
Java and Python Code for Radix Sort
Java Code
import java.util.Arrays;
public class RadixSort {
// Main function to implement radix sort
public static void radixSort(int[] arr) {
int maxNumber = findMax(arr);
int numDigits = numberOfDigits(maxNumber);
for (int digitPlace = 1; maxNumber / digitPlace > 0; digitPlace *= 10) {
countingSortByDigit(arr, digitPlace);
}
}
// Function to find the maximum number in the array
private static int findMax(int[] arr) {
int max = arr[0];
for (int num : arr) {
if (num > max) {
max = num;
}
}
return max;
}
// Function to count the number of digits in a number
private static int numberOfDigits(int number) {
int count = 0;
while (number != 0) {
number /= 10;
count++;
}
return count;
}
// Function to perform counting sort on the array based on the digit place
private static void countingSortByDigit(int[] arr, int digitPlace) {
int n = arr.length;
int[] output = new int[n];
int[] count = new int[10];
Arrays.fill(count, 0);
for (int i = 0; i < n; i++) {
int digit = (arr[i] / digitPlace) % 10;
count[digit]++;
}
for (int i = 1; i < 10; i++) {
count[i] += count[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
int digit = (arr[i] / digitPlace) % 10;
output[count[digit] - 1] = arr[i];
count[digit]--;
}
System.arraycopy(output, 0, arr, 0, n);
}
public static void main(String[] args) {
int[] arr = {329, 457, 657, 839, 436, 720, 355};
System.out.println("Original Array: " + Arrays.toString(arr));
radixSort(arr);
System.out.println("Sorted Array: " + Arrays.toString(arr));
}
}
Python Code
def radix_sort(arr):
def find_max(arr):
max_num = arr[0]
for num in arr:
if num > max_num:
max_num = num
return max_num
def number_of_digits(number):
count = 0
while number != 0:
number //= 10
count += 1
return count
def counting_sort_by_digit(arr, digit_place):
n = len(arr)
output = [0] * n
count = [0] * 10
for i in range(n):
digit = (arr[i] // digit_place) % 10
count[digit] += 1
for i in range(1, 10):
count[i] += count[i - 1]
for i in range(n - 1, -1, -1):
digit = (arr[i] // digit_place) % 10
output[count[digit] - 1] = arr[i]
count[digit] -= 1
for i in range(n):
arr[i] = output[i]
max_number = find_max(arr)
num_digits = number_of_digits(max_number)
digit_place = 1
while max_number // digit_place > 0:
counting_sort_by_digit(arr, digit_place)
digit_place *= 10
# Test the radix sort function
arr = [329, 457, 657, 839, 436, 720, 355]
print("Original Array:", arr)
radix_sort(arr)
print("Sorted Array:", arr)
Time and Space Complexity of Radix Sort Algorithm
- Time Complexity: O(d × (n + k)) where d is the number of digits, n is the number of elements in the array, and k is the range of the digits (0-9 for the decimal system).
- Space Complexity: O(n + k), primarily due to the space used by the counting sort algorithm.
Radix Sort is efficient for large datasets where the number of digits (d) is significantly smaller than the number of elements (n). It is particularly useful for sorting numbers, strings, or other data types with fixed-length representations.
Related Articles
Frequently Asked Questions
In Radix Sort Algorithm each digit is arranged from least to most significant. In base 10 the one’s place digits would be sorted first, followed by the ten’s place, and so on.
When the range of the input data is greater than the number of data points, radix sort loses efficiency. It’s not as space-efficient as compared to other sort algorithms like Quick Sort because it takes up more room.
(i) Sorting Large Databases:
- Application: Suppose a government agency has a database of social security numbers (SSNs) and needs to sort them.
- How It Works: Each SSN has a fixed length, typically nine digits. Radix sort can efficiently sort this list by processing each digit of the SSNs, starting from the least significant digit (rightmost) to the most significant digit (leftmost).
(ii) Processing Postal Codes:
- Application: A logistics company wants to sort addresses by postal codes for efficient delivery route planning.
- How It Works: Postal codes are fixed-length alphanumeric strings. Radix sort can process each character in the postal code, starting from the least significant position to the most significant, ensuring the addresses are sorted correctly.
(iii) Sorting Telephone Numbers:
- Application: A telecom company needs to organize a list of customer phone numbers.
- How It Works: Phone numbers have a fixed length (e.g., 10 digits in the US). Radix sort processes each digit of the phone numbers from the least significant to the most significant digit, resulting in an efficiently sorted list.
While the range of values matters for counting sort, the number of digits and the base matter for radix sort. Radix sort may be slower than counting sort if the range of values is larger than the list size.