Introduction
Shear stress is a fundamental concept in Physics and Engineering that describes the force per unit area acting parallel to the surface of a material. Unlike normal stress, which acts perpendicular to the surface, shear-stress acts tangentially, causing layers of material to slide past each other.
This phenomenon plays a crucial role in various fields, including Civil Engineering, Materials Science, and Fluid Mechanics.
Key Points
- Definition: Force per unit area acting parallel to a surface.
- Units: Measured in Pascals (Pa) or Newtons per square meter (N/m²).
- Distinct from Normal Stress: Normal stress acts perpendicular, while shear stress acts parallel to the surface.
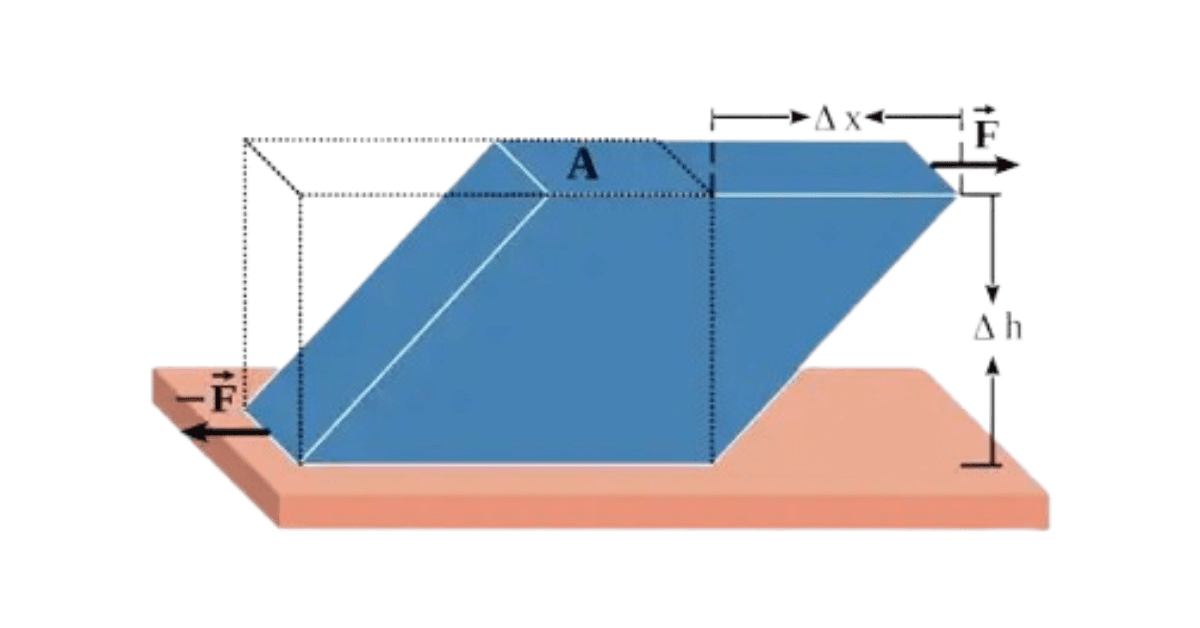
Mathematical Representation of Shear Stress
Shear Stress (τ) can be mathematically expressed as:
τ = F/A
Where:
- τ is the shear stress.
- F is the force applied parallel to the surface.
- A is the area over which the force is distributed.
This equation shows that shear stress is directly proportional to the applied force and inversely proportional to the area. Therefore, increasing the force or decreasing the area increases the shear-stress.
Key Points:
- Direct Proportionality: It increases with an increase in applied force.
- Inverse Proportionality: This decreases with an increase in the surface area.
Types of Shear Stress
This can be categorized into two main types based on the nature of the material and the type of force applied:
- Direct Shear Stress: This occurs when two forces are applied in opposite directions, causing the material to experience a direct shearing force. It is commonly observed in structural elements such as beams, bolts, and shafts.
- Torsional Shear Stress: This type of shear-stress occurs when a twisting force (torque) is applied to a material, causing it to experience a rotational force. Torsional stress is often encountered in shafts and other cylindrical objects subjected to twisting forces.
Key Points:
- Direct: Observed in beams, bolts, and similar structural elements.
- Torsional: Observed in shafts and cylindrical objects under rotational force.
Stress in Fluids
In fluids, this kind of stress is essential in understanding viscosity, which is the measure of a fluid’s resistance to flow.
When a fluid flows over a surface, the layers of the fluid experience shear stress due to the velocity gradient between them.
This is particularly important in understanding fluid dynamics and the behavior of liquids and gases in different environments.
Key Points:
- Fluid Viscosity: It is directly related to a fluid’s viscosity.
- Velocity Gradient: The difference in velocity between fluid layers creates shear stress.
Importance of Shear Stress in Engineering
This type of stress is a critical factor in the design and analysis of structural elements. Engineers must consider shear stress to ensure the safety and stability of structures. For example:
- Beam Design: Beams in buildings and bridges must be designed to withstand shear forces to prevent failure.
- Material Selection: Materials are selected based on their shear strength, which is the maximum stress they can endure before failing.
- Failure Analysis: Understanding shear stress helps in analyzing structural failures and preventing future incidents.
Key Points:
- Structural Integrity: This analysis ensures the safety of structures.
- Material Strength: Materials are chosen based on their ability to withstand this kind of stress.
Applications of Shear Stress
Shear stress has numerous applications across different fields:
- Civil Engineering: In designing buildings, bridges, and other structures, calculations are essential to prevent structural failure.
- Mechanical Engineering: This is considered in the design of mechanical components like gears, shafts, and bolts to ensure they can withstand operational forces.
- Geology: It plays a role in understanding tectonic movements and the deformation of earth’s crust.
- Medicine: In biomechanics, this phenomenon affects blood flow and can influence the health of blood vessels.
Key Takeaways:
- Civil Engineering: Critical in preventing structural failure.
- Mechanical Engineering: Ensures the durability of components.
- Geology: Helps in understanding earth’s deformation.
- Medicine: Influences blood flow and vascular health.
Conclusion
It is a pivotal concept in physics and engineering, affecting various aspects of material behavior, structural design, and fluid dynamics. Understanding shear stress and its implications allows engineers and scientists to design safer structures, develop more efficient mechanical systems, and explore the dynamics of fluids and materials under different conditions.
Frequently Asked Questions
“A type of stress that acts coplanar with cross section of material” is the definition of shearing stress. Shear forces give rise to shear stress. They are the two forces of equal magnitude and opposite direction acting on opposing sides of a body.
When a deforming force is applied to a surface at a right angle, the result is tensile stress. Shear-stress, on the other hand, results from the application of a deforming force parallel to the surface.
This kind of strain is created when the body’s shape is altered by the deforming force. It can be defined as the ratio of a layer’s displacement to its separation from the fixed layer.
It is merely a ratio of the material’s cross sectional area to the external forces. Shear stresses are applied parallel to the cross section, whereas normal stresses are applied perpendicular to the cross section.