The Fermi Dirac Distribution Function is a fundamental concept in the field of engineering physics, playing a crucial role in the study of quantum mechanics and the behavior of fermions like electrons. It describes the probability that a quantum state is occupied by a fermion, such as an electron, at a given energy and temperature.
Table of Contents
Introduction
At the time of proposing the classical free electron theory, Drudge assumed the electrons were distinguishable and all the electrons would absorb the energy supplied. So, he used the Maxwell-Boltzmann distribution function, which states that the average number if particles in a state of energy E is proportional to e – E/kBT.
This statistical function helps describe how fermions such as electrons are distributed over energy states in a system, particularly at different temperatures. It is essential for designing and understanding the electronic properties of materials, including metals and semiconductors.
What is the Fermi Dirac Distribution Function?
The Fermi Dirac Distribution Function, denoted as ๐(๐ธ), predicts the probability that a quantum state at a certain energy is occupied by a fermion. This function is especially important because fermions obey the Pauli Exclusion Principle, which states that no two identical fermions can occupy the same quantum state simultaneously.
Formula and Explanation
The Mathematical expression for the Fermi Dirac Distribution Function is:
๐(๐ธ) = 1/e(E – EF)/(kBT) + 1
Where:
- E represents the energy of the quantum state of the particle.
- EF is the chemical potential or Fermi energy at absolute zero temperature.
- ๐๐ต is the Boltzmann constant.
- T is the absolute temperature in kelvin.
Key Points of the Function
1. Energy Levels Relative to the Fermi Level:
- If E = EF, ๐(๐ธ) = 0.5.
- ๐(๐ธ) = 0.5.
- If E > EF, ๐(๐ธ) decreases towards 0 as the energy increases.
- If E < EF, ๐(๐ธ) increases towards 1 as the energy decreases.
2. Temperature Effects:
- At T = 0K (absolute zero), the function becomes a step function: it is 1 if E < EF and 0 if E > EF.
- As T increases, the function smooths out around EF, indicating that higher energy states have a probability of being occupied due to thermal excitation.
Visualizing the Fermi Dirac Distribution Function
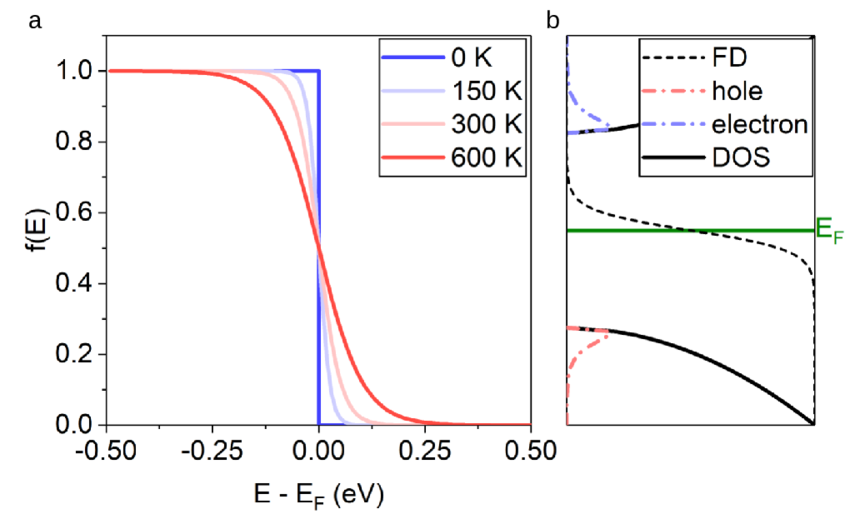
The behavior of the Fermi-Dirac distribution function can be effectively illustrated through graphs that depict how the occupation probability varies with energy at different temperatures.
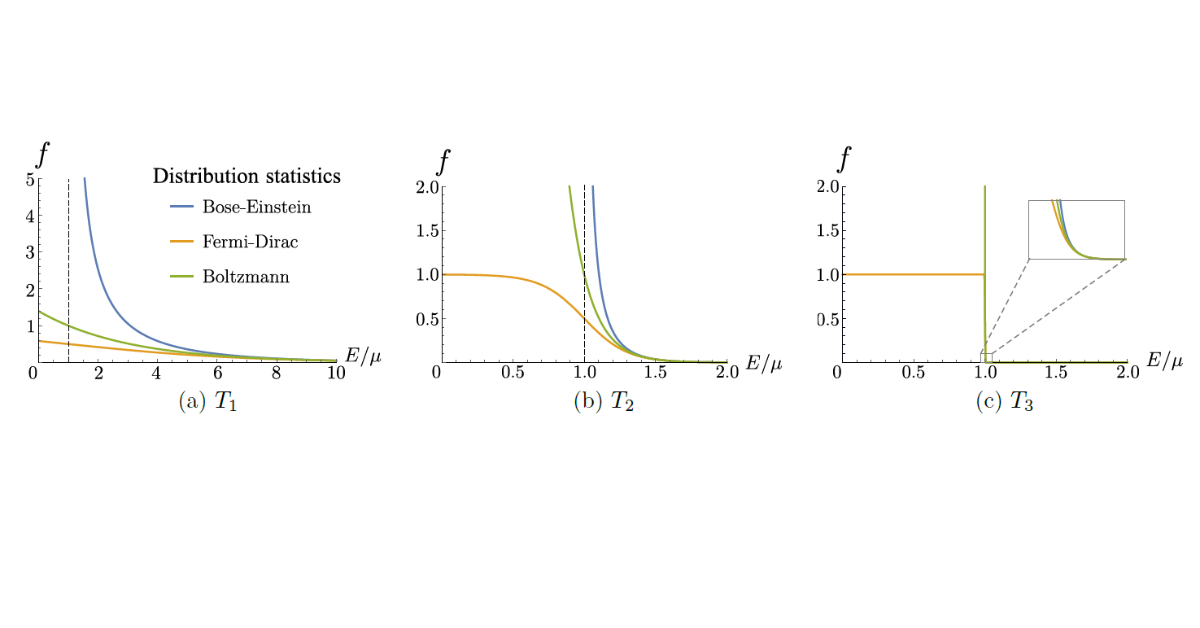
The above image shows the occupancy ๐(๐ธ) determined by the three equilibrium distributions. While they converge at E, their behavior is dramatically different for low temperatures T3 < T2 < T1.
- Graph of the Fermi Dirac Distribution: Shows how the probability of occupation changes with energy at different temperatures.
- Energy Band Diagram: Illustrates the Fermi level in relation to the conduction and valence bands in a semiconductor.
Here is a detailed educational chart showing the Fermi Dirac distribution function at different temperatures. This visual illustrates how the occupation probability changes with energy:
- At absolute zero (0K), the distribution is a sharp step function.
- At room temperature, the curve is smoother, indicating some electrons are thermally excited above the Fermi level.
- At high temperature, the curve becomes even smoother, showing increased thermal excitation.
These graphs help visualize how temperature affects electron distribution in materials, crucial for understanding various physical properties in engineering and physics.
Applications in Engineering
- Semiconductors: Understanding and manipulating the Fermi level in semiconductors is crucial for designing electronic devices like transistors and diodes.
- Metals: The distribution helps explain the electrical and thermal properties of metals.
- Superconductivity: Insights into how electrons fill energy states contribute to theories and applications of superconductivity.
Effect of Temperature on Fermi Function
Since most of the measurements are made at room temperature, and we must consider the effect of temperature on the electron gas. So, it is important to know the variation of Fermi Dirac Distribution function with respect to temperature in the following cases.
Case I: At absolute zero (T = 0K) and E < EF. Substituting in the above equation, we get
๐(๐ธ) = 1/(1 + e -โ), since e -โ = 0
๐(๐ธ) = 1
The distribution function ๐(๐ธ) = 1 means that all the energy levels below the Fermi energy EF are fully occupied by electrons leaving the upper levels vacant, i.e., there is 100% probability of finding an electron below the Fermi energy level.
Case II: At absolute zero (T = 0K) and E > EF. Substituting in the above equation, we get
๐(๐ธ) = 1/(1 + eโ), since eโ = โ
๐(๐ธ) = 1/(1 + โ)
๐(๐ธ) = 1/โ = 0
The result clearly indicates that at T = 0K, and the energy levels above Fermi level EF is not occupied by electrons, i.e., they are vacant. There is 0% probability of finding the electron above Fermi level at absolute zero.
Case III:ย At temperatures slightly above 0K (T > 0K) and E = EF. Substituting this condition in the above equation, we get
๐(๐ธ) = 1/(1 + e0) = 1/(1 + 1) = 1/2 = 0.5
At temperatures above 0K, i.e., at room temperature and at E = EF there is only 50% probability for an electron to occupy Fermi energy level.
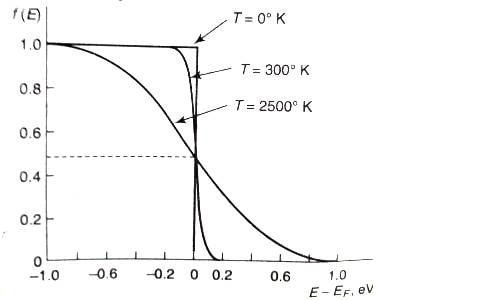
Case IV:ย At high temperatures, ๐๐ตT >> EF or T โ โ.ย At high temperature, electrons are excited to vacant levels above the Fermi level. As a result, the probability of finding the electrons above EF becomes greater than zero, as shown in the below image.
At high temperatures, the electrons lose their quantum mechanical character and obey the classical Boltzmann distribution function. Therefore, at higher temperatures, the choice between the classical and quantum statistics is meaningless as both give similar results.
The below image shows the variation of Fermi function ๐(๐ธ) for different temperature and energy levels.
Conclusion
The Fermi Dirac Distribution Function is a cornerstone of quantum mechanics and materials science, helping engineers and scientists predict and manipulate the electronic properties of materials. Understanding this function is essential for advancements in technology, from microelectronics to quantum computing. This guide aims to provide a foundational understanding of how the Fermi Dirac distribution influences the world of engineering physics.
Related Articles
FAQ's
A mathematical representation of the probability distribution of the energies of the quantum states that electrons can exist in at a specific temperature is the Fermi-Dirac distributionย function. It explains the behavior of electrons inside metal solids as their temperature rises.
In terms of physics, it means that: ๐(๐ธ) is the potential of an electron occupying an energy state at energy E. In other words, ๐(๐ธ) is the probability that an electron is in this state, and 1 – ๐(๐ธ) is the probability that is vacant.
Based on the theory that metals contain free electrons that constitute a perfect gas known as electron gas, Fermi Dirac statistics has numerous applications in the study of thermal and electrical conductivities, thermoelectricity, thermionic and photoelectric effects, specific heat of metals, etc.
The probability of electron occupation in a given energy state (Ei) at thermal equilibrium is known as the Fermi function, or ๐(๐ธ). The Boltzmann constant is ๐๐ต, the energy of the ith state is Ei, and the Fermi energy is EF.
1 thought on “Unlock the Secrets of Fermi Dirac Distribution Function”