Mastering Depth First Search Algorithm

Introduction to Depth First Search Algorithm

In this blog, we will explore the Depth First Search Algorithm or DFS in data structures. DFS is a recursive algorithm used to traverse all the vertices of a tree or graph. The DFS algorithm starts with an initial node of graph G and explores deeper until it finds the goal node or a node with no children.

Due to its recursive nature, the DFS algorithm can be efficiently implemented using a stack data structure. The implementation process of DFS is similar to that of the Breadth First Search (BFS) algorithm.

Algorithm Steps

Here are the step-by-step instructions to implement the DFS traversal:

Initialize a stack with the total number of vertices in the graph.
Choose any vertex as the starting point of traversal and push it onto the stack.
Push a non-visited vertex (adjacent to the vertex on the top of the stack) onto the top of the stack.
Repeat steps 3 and 4 until no vertices are left to visit from the vertex on the top of the stack.
If no vertex is left, backtrack and pop a vertex from the stack.
Repeat steps 2, 3, and 4 until the stack is empty.

By then, all the vertices in the same connected component as the starting vertex have been visited. If unvisited vertices still remain, the depth-first search must be restarted at any one of them.

It is convenient to use a stack to trace the operation of depth-first search algorithm. Explanation is given below 👇.

The algorithm eventually halts after backing up to the starting vertex, with the latter being a dead end.

Pseudocode Example

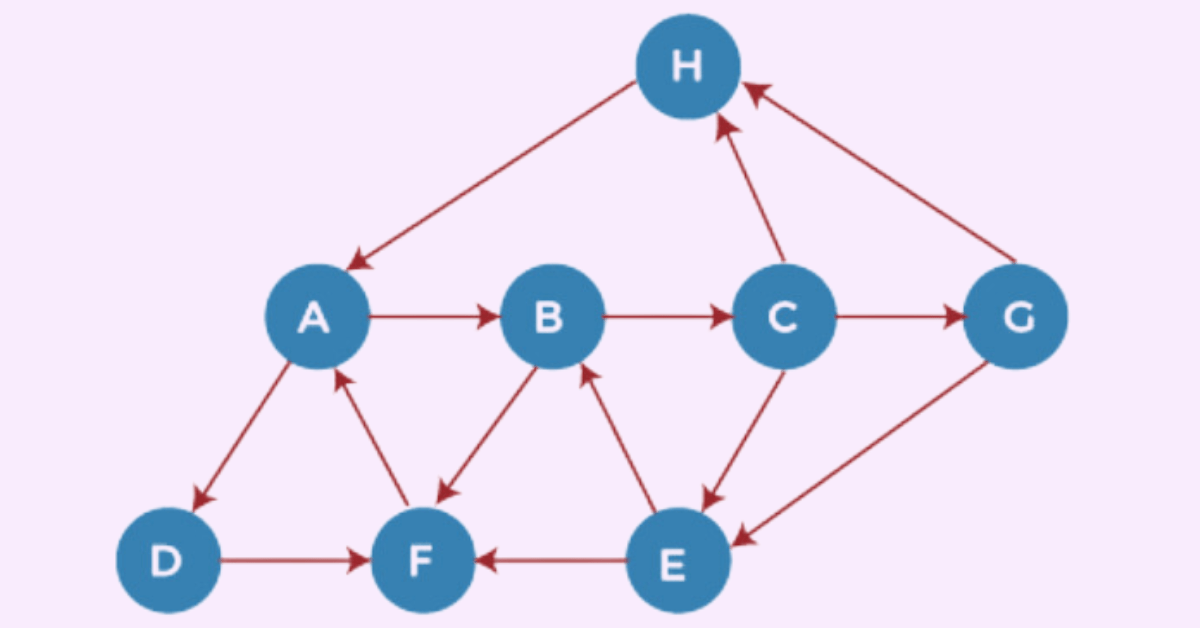
Let’s understand the working of the DFS algorithm using an example. Consider a directed graph with 7 vertices.

Adjacency List:

A: B, D
B: C, F
C: E, G, H
D: E, H
E: B, F
F: A
G: F
H: A

Starting from Node H:

Step 1: Push H onto the stack.
Step 2: POP H, print it, and PUSH all ready neighbors.
Step 3: POP A, print it, and PUSH all ready neighbors.
Step 4: POP D, print it, and PUSH all ready neighbors.
Step 5: POP F, print it, and PUSH all ready neighbors.
Step 6: POP B, print it, and PUSH all ready neighbors.
Step 7: POP C, print it, and PUSH all ready neighbors.
Step 8: POP G, print it, and PUSH all ready neighbors.
Step 9: POP E, print it, and PUSH all ready neighbors.

Now, all the graph nodes have been traversed, and the stack is empty.

DFS Algorithm

//Implements a depth-first search traversal of a given graph

//Input: Graph G = (V,E)

//Output: Graph G with its vertices marked with consecutive integers in the order they are first encountered by the DFS traversal mark each vertex in V with 0 as a mark of being “unvisited”

count ← 0

for each vertex v in V do

if v is marked with 0

dfs(v)

//visits recursively all the unvisited vertices connected to vertex v by a path and numbers

// them in the order they are encountered via global variable count

count ← count + 1; //mark v with count

for each vertex w in V adjacent to v do

if w is marked with 0

dfs(w)

Applications of Depth First Search Algorithm

The DFS algorithm has several applications:

Topological Sorting: Ordering of vertices such that for every directed edge (u,v), vertex u comes before vertex v in the ordering.
Path Finding: Finding a path between two vertices.
Cycle Detection: Detecting cycles within a graph.
Puzzle Solutions: Solving one-solution puzzles.
Bipartiteness Checking: Determining whether a graph can be colored with two colors such that no two adjacent vertices have the same color.

DFS Visualization Tool

DFS Code Snippets

Java Code Snippet:

				
					import java.util.*;

public class DFS {
    private LinkedList<Integer> adjLists[];
    private boolean visited[];

    // Graph creation
    DFS(int vertices) {
        adjLists = new LinkedList[vertices];
        visited = new boolean[vertices];

        for (int i = 0; i < vertices; i++)
            adjLists[i] = new LinkedList<Integer>();
    }

    // Add edges
    void addEdge(int src, int dest) {
        adjLists[src].add(dest);
    }

    // DFS algorithm
    void DFS(int vertex) {
        visited[vertex] = true;
        System.out.print(vertex + " ");

        Iterator<Integer> ite = adjLists[vertex].listIterator();
        while (ite.hasNext()) {
            int adj = ite.next();
            if (!visited[adj])
                DFS(adj);
        }
    }

    public static void main(String args[]) {
        DFS g = new DFS(4);

        g.addEdge(0, 1);
        g.addEdge(0, 2);
        g.addEdge(1, 2);
        g.addEdge(2, 0);
        g.addEdge(2, 3);
        g.addEdge(3, 3);

        System.out.println("Depth First Traversal:");
        g.DFS(2);
    }
}

C++ Code Snippet:

				
					#include<iostream>
#include<list>

using namespace std;

class Graph {
    int numVertices;
    list<int> *adjLists;
    bool *visited;

public:
    Graph(int vertices);
    void addEdge(int src, int dest);
    void DFS(int vertex);
};

// Initialize graph
Graph::Graph(int vertices) {
    numVertices = vertices;
    adjLists = new list<int>[vertices];
    visited = new bool[vertices];
    fill(visited, visited + vertices, false);
}

// Add edges
void Graph::addEdge(int src, int dest) {
    adjLists[src].push_back(dest);
}

// DFS algorithm
void Graph::DFS(int vertex) {
    visited[vertex] = true;
    cout << vertex << " ";

    list<int>::iterator i;
    for(i = adjLists[vertex].begin(); i != adjLists[vertex].end(); ++i)
        if(!visited[*i])
            DFS(*i);
}

// Main function
int main() {
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    cout << "Depth First Traversal starting from vertex 2:\n";
    g.DFS(2);

    return 0;
}

Output:

For both implementations, assuming the graph connections and starting vertex (vertex 2) are the same, the output will be:

Depth First Traversal starting from vertex 2:
2 0 1 3

Time Complexity of DFS Algorithm

It is not difficult to see that this algorithm is in fact, quite efficient since it takes just the time proportional to the size of the data structure used for representing the graph in question.

Time Complexity: O(V+E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: O(V).

Conclusion

In this blog, we delved into the Depth First Search algorithm, exploring its technique, a practical example, time complexity, and its implementation using the python programming language. Additionally, we highlighted various applications where the Depth First Search algorithm proves to be invaluable.

We hope that this example has provided a better and clear understanding of the Depth First Search algorithm. We hope you found it helpful and insightful. Do let us know know in the comments section below to help us improve.

FAQ's

1. Difference between DFS and BFS.

	DFS	BFS
Data structure	a stack	a queue
Number of vertex orderings	two orderings	one ordering
Edge types (undirected graphs)	tree and back edges	tree and cross edges
Applications	connectivity, acyclicity, articulation points	connectivity, acyclicity, minimum-edge paths
Efficiency for adjacency matrix	Θ (\|V\|²)	Θ (\|V\|²)
Efficiency for adjacency lists	Θ (\|V\| + \|E\|)	Θ (\|V\| + \|E\|)

2. What is depth first search algorithm and backtracking?

If feasible, it involves moving forward and, if not, going backward to thoroughly search every node.

3. Is backtracking DFS or BFS?

Backtracking uses DFS to traverse the solution space. It is Explained above👆.

4. What is depth first search in Python?

An algorithm for tree traversal on graph or tree data structures is called depth-first search (DFS). Recursion and data structures like dictionaries and sets make it simple to implement.

7 thoughts on “Best Depth First Search Algorithm | DFS in Python”

Pingback: Heap Sort Algorithm | Conquer Data Sorting
Pingback: Warshall's Algorithm | Floyd-Warshall Algorithm
Pingback: Kadane’s Algorithm | Maximum Sum of Contiguous Subarray
Pingback: Karnaugh Map Solver
Audra FitzRoy
11 August 2024 at 1:51 AM
This was a very good post. Check out my web page 81N for additional views concerning about Cosmetics.
Pingback: Mastering the Powerful Three-Schema Architecture in DBMS
Pingback: Solving the Fake Coin Problem | 3 Comprehensive Methods

Best Depth First Search Algorithm | DFS in Python