Table of Contents
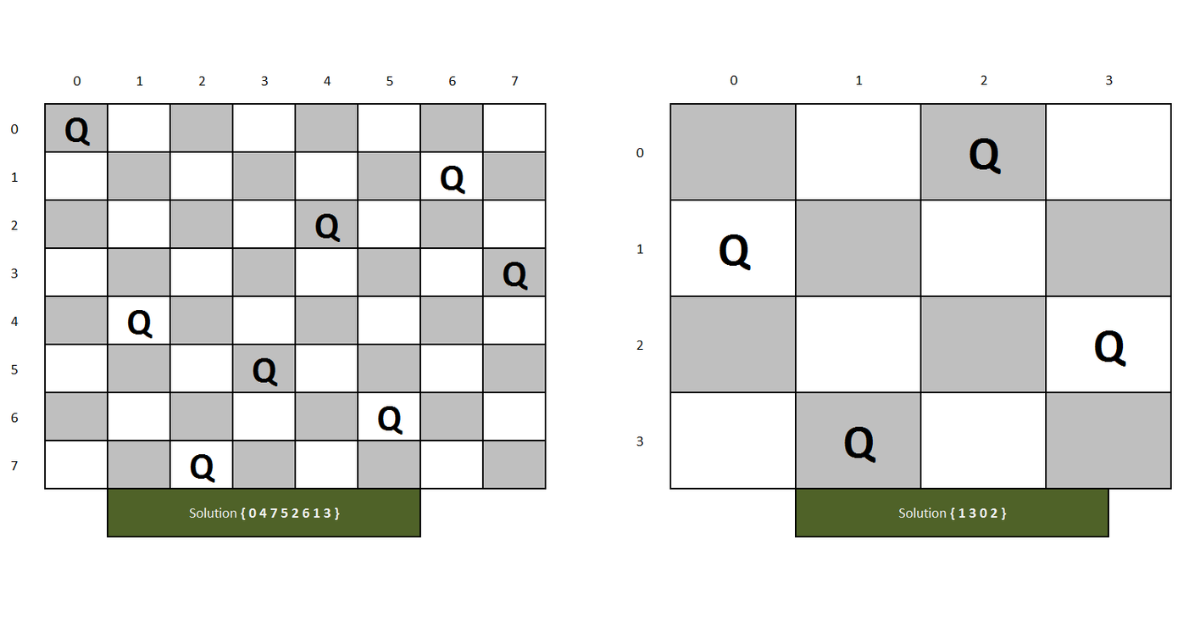
The n queens problem using backtracking is to place the queens on an n x n chessboard so that no two queens attack each other by being in the same row or in the same column or on the same diagonal. For n = 1, the problem has a trivial solution, and it is easy to see that there is no solution for n = 2 and n = 3. So let us consider the four-queens problem and solve it by the backtracking technique.
Since each of the four queens has to be placed in its own row, all we need to do is to assign a column for each queen on the board presented below.
n Queens Problem using Backtracking Method
- We start with the empty board and then place queen 1 in the first possible position of its row, which is in column 1 of row 1.
- Then we place queen 2, after trying unsuccessfully columns 1 and 2, in the first acceptable position for it, which is square (2, 3), the square in row 2 and column 3.
- This proves to be a dead end because there is no acceptable position for queen 3. So, the algorithm backtracks and puts queen 2 in the next possible position at (2, 4).
- Then queen 3 is placed at (3, 2), which proves to be another dead end. The algorithm then backtracks all the way to queen 1 and moves it to (1, 2).
- Queen 2 then goes to (2, 4), queen 3 to (3, 1), and queen 4 to (4, 3), which is a solution to the problem. The state-space tree of this search is shown below.
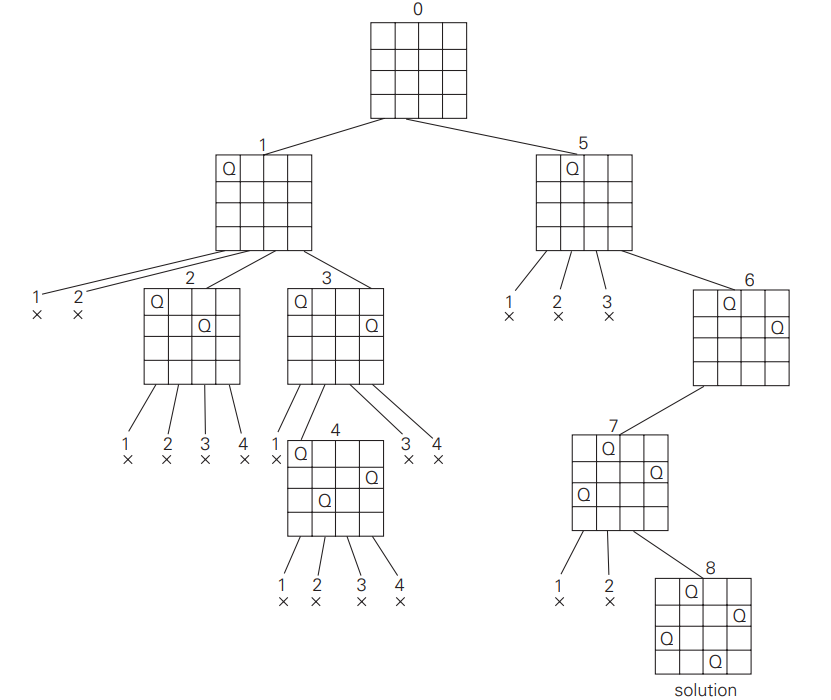
In the above figure, x denotes an unsuccessful attempt to place a queen in the indicated column. The numbers above the nodes indicate the order in which the nodes are generated.
Note: Alternatively, we can use the board’s symmetry for this purpose.
Finally, it should be pointed out that a single solution to the n queens problem using backtracking for any n ≥ 4 can be found in linear time. Such positions can also be found by applying some general algorithm design strategies.
n Queens Problem in Python
# Python code to solve N Queen
# Solution using backtracking
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print(board[i][j], end=' ')
print()
# A utility function to check if a queen can be placed on board[row][col]. Note that this function is called when "col",
# queens are already placed in columns from 0 to col -1. So we need to check only left side for attacking queens.
def isQSafe(board, row, col):
# Check particular row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check for upper diagonal on left side
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check for lower diagonal on left side
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
if col >= N:
return True
# Considering the particular column and try placing the queens in all rows one by one
for i in range(N):
if isQSafe(board, i, col):
board[i][col] = 1
if solveNQUtil(board, col + 1) == True:
return True
board[i][col] = 0
return False
# This function solves the N Queen problem using Backtracking. It mainly uses solveNQUtil() to solve the problem.
def solveNQ():
board = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
if solveNQUtil(board, 0) == False:
print("Solution does not exist")
return False
printSolution(board)
return True
solveNQ()
Output
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
n Queens Problem in Java
public class NQueenProblem {
final int N = 4;
void printSolution(int board[][]) {
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
System.out.print(" " + board[i][j] + " ");
System.out.println();
}
}
boolean isSafe(int board[][], int row, int col) {
int i, j;
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
boolean solveNQUtil(int board[][], int col) {
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQUtil(board, col + 1) == true)
return true;
board[i][col] = 0;
}
}
return false;
}
boolean solveNQ() {
int board[][] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
System.out.println("Solution does not exist");
return false;
}
printSolution(board);
return true;
}
public static void main(String[] args) {
NQueenProblem Queen = new NQueenProblem();
Queen.solveNQ();
}
}
Output
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
Solving any n Queens Problem using Backtracking
Note: For solving any n Queens Problem using backtracking, just replace N by the number you want to solve. For example: N=8, since there are 8 queens replace N=8 and in the solveNQ() method add 8 x 8 Array, check below on how to add?
{ { 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0, 0, 0, 0 } };
🙌You are done! Similarly you can solve for any n queens problem using Java and Python by replacing N and the array.
Disclaimer: The concept of n Queens Problem using backtracking is explained in the code.
FAQ's
N Queens must be arranged on a N x N chessboard in the N-Queens Problem so that no two queens can pose a threat to one another.
Four queens on a 4 x 4 chessboard make up the 4-queens problem. Placing the four queens on the chessboard so that they cannot attack one another is the aim.
Placing 16 queens on a chessboard so that no two queens attack the other is known as the “16-Queens Problem.”
Since every queen needs to be tested in every column of every row in the worst case, the algorithm’s time complexity can be written as O(N!).
n Queens Problem uses backtracking method. The concept of n Queens Problem using Backtracking, is explained above.👆