Warshall’s algorithm, also known as the Floyd-Warshall Algorithm, is a graph algorithm used for finding the shortest paths between all pairs of vertices in a weighted graph. This algorithm works with both directed and undirected graphs, and it is especially helpful for dense graphs. It can handle graphs with negative edge weights but not with negative weight cycles.
You can check how the digraph, its adjacency matrix, and its transitive closure looks in the below image.
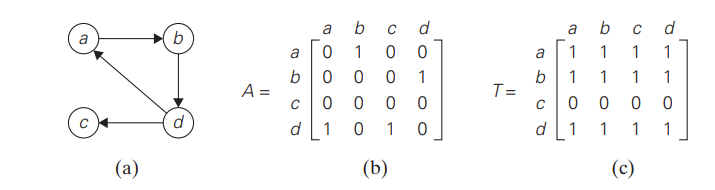
Warshall’s algorithm constructs the transitive closure through a series of n × n boolean matrices say:
R(0) ,..., R(k−1) , R(k),... R(n)
Thus, the series starts with R(0) , which does not allow any intermediate vertices in its paths and is nothing other than the adjacency matrix of the digraph.
Rule for Changing zeros in Warshall’s Algorithm
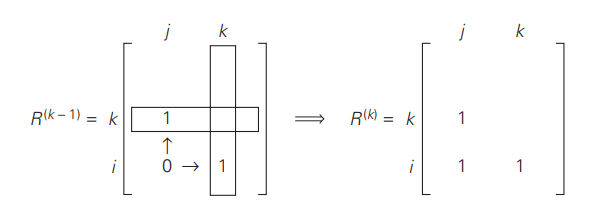
- In the first, the list of its intermediate vertices does not contain the kth vertex. Then this path from vi to vj has intermediate vertices numbered not higher than k − 1, and therefore r(k−1) ij is equal to 1 as well.
- The second possibility is that the path does contain the kth vertex vk among the intermediate vertices. Without loss of generality, we may assume that vk occurs only once in that list.
vi , vertices numbered ≤ k − 1, vk , vertices numbered ≤ k − 1, vj .
From the above two cases the formula can be written as;
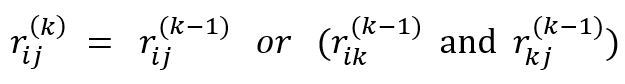
- If an element rij is 1 in R(k−1) , it remains 1 in R(k).
- If an element rij is 0 in R(k−1) , it has to be changed to 1 in R(k) if and only if the element in its row i and column k and the element in its column j and row k are both 1’s in R(k−1).
The application of Warshall’s algorithm to the digraph is shown in the below Image.
Pseudocode
Warshall(A[1..n, 1..n])
//Implements Warshall’s algorithm for computing the transitive closure
//Input: The adjacency matrix A of a digraph with n vertices
//Output: The transitive closure of the digraph
R(0) ← A
for k ← 1 to n do
for i ← 1 to n do
for j ← 1 to n do
R(k)[i, j ] ← R(k−1) [i, j ] or (R(k−1) [i, k] and R(k−1) [k, j ])
return R(n)

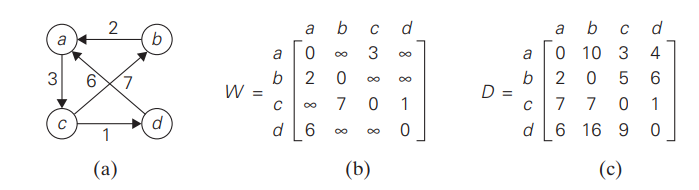
Time Complexity
The time complexity of Warshall’s algorithm is O(n3), where n is the number of vertices in the graph. This makes it efficient for relatively small graphs but less suitable for very large graphs due to its cubic complexity.
Use Cases:
- Network Routing: Finding the shortest path in a network.
- GIS Applications: Calculating shortest paths between geographical locations.
- Dynamic Programming Problems: Solving problems involving paths and distances between nodes.
Warshall's Algorithm Visualization Tool
Compare the transitive closure using Warshall's Algorithm
Properties and Features
- Handles Negative Weights:
- Can handle negative edge weights but not negative weight cycles.
- If a negative weight cycle exists, the algorithm can detect it because the distance from the vertex to itself would become negative.
- Complete Solution:
- Provides the shortest path distances between all pairs of vertices, making it a comprehensive solution for many network analysis problems.
- Simplicity:
- The algorithm is relatively simple to implement compared to other algorithms which finds the shortest paths, though it is not as efficient for large graphs with non-negative weights as Dijkstra’s Algorithm.
Applications
- Used in network routing protocols to find the shortest path information required between all pairs of nodes.
- Helps in planning and optimizing routes within urban transportation networks.
- Useful in various applications in computer science and operations research where complete path information is needed.
Related Articles
FAQ's
In a weighted graph, it is employed to determine the shortest paths between every pair of nodes. This algorithm is a flexible tool for resolving a variety of network and connectivity issues because it is very efficient and can handle graphs with both positive and negative edge weights.
Dijkstra’s Algorithm is suitable for solving the single-source shortest path problem with non-negative weights using a greedy approach.
Warshall’s Algorithm (often referred to as the Floyd-Warshall algorithm) is used for solving the all-pairs shortest path problem using a dynamic programming approach that can handle negative weights (but no negative cycles).
Since the original Warshall’s algorithm only looks for a graph’s transitive closure and doesn’t make use of edge weight information, it is actually simpler. This algorithm, plus extra considerations regarding such weights, is essentially Floyd’s algorithm.